9016. Binary search
A sorted array of
n integers is given. It is necessary to answer q queries:
whether the given number x is present in the array.
Input. The first line
contains two integers n and q (n, q ≤ 106). The second line contains n
integers sorted in ascending order. Each of the following q lines
contains one number x. All numbers in the array do not exceed 109
by absolute value.
Output. For each query, print “YES” on
a separate line if the number x is present in the array, and “NO”
otherwise.
|
Sample
input 1 |
Sample
output 1 |
|
6 3 2 4 4 8 11 14 10 4 2 |
NO YES YES |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
8 4 -8 -8 -1 1 3 4 6 8 4 10 -4 -8 |
YES NO NO YES |
SOLUTION
binary search
Algorithm
analysis
In this problem, it is
required to find a number in a sorted array, which can be done using binary
search.
Let m be a sorted array
of length n, consisting of integers. The function binary_search(m, m
+ n, x) returns true if number x is present in the array. Reading the input array takes O(n), and handling q queries takes O(qlog2n).
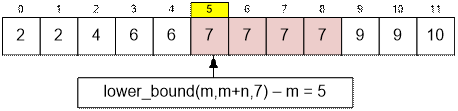
The lower_bound function returns a
pointer to the first position where the element x can be inserted without violating the sorted order of the array.
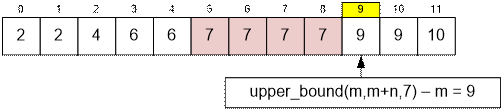
The upper_bound function returns a
pointer to the last position where the element x can be inserted without violating the sorted order of the array.
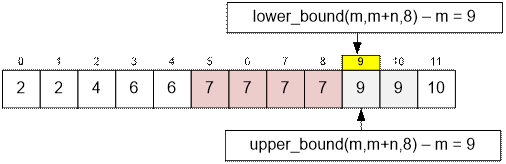
If lower_bound(m, m + n,
x) ≠ upper_bound(m, m
+ n, x), then the number x
is present in the array. Otherwise, the number x is not in the array.
The Java function Arrays.binarySearch() returns
the index of the found element in the array. If the array contains multiple
identical keys, it returns the index of any one of them.

If x
is not present in the array m, the function Arrays.binarySearch(m, x) returns the value –pos – 1, where pos is the index of the first element greater than x. If x is greater than all elements in the array m, then pos = m.length.

The bisect function in Python is used for performing
binary search in sorted sequences. It helps find the insertion point for an
element in a sorted list to maintain the order of the list. This can be useful,
for example, for optimizing the insertion of new elements into an ordered list
or for determining where to insert an element in an array to keep it sorted.
bisect provides two main functions:
·
bisect.bisect_left(lst, x, lo = 0, hi = len(lst)).
This function finds the
insertion point for element x in the sorted list lst. If the
element is already present in the list, bisect_left will return the index of the first occurrence of x.
If the element is absent, the function will return the index where x can
be inserted without breaking the sorting order.
·
bisect.bisect_right(lst, x, lo = 0, hi = len(lst)).
Similar to bisect_left, but it returns the index for inserting element x
after the existing occurrences of x in the list lst.
Both functions accept optional arguments lo
and hi, which define the search range within the list. By default, lo = 0, and hi = len(lst).
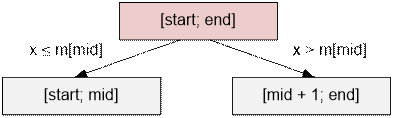
Implementation of own binary search. Suppose we need to find the element x
in the array m within the range [start;
end]. Divide the segment in half, setting
mid = (start + end) / 2. If x > m[mid],
then the element x is in the range [mid + 1; end]. Otherwise, continue the search in the range [start; mid].
Data structures set. Insert the numbers from the
input array into a set<int> s. If a number appears multiple times in the array, it will be added to
the set only once. The result of
checking for the presence of a given element in the array remains unchanged.
An element x is present in the set (and in the input array) if s.find(x) != s.end().
Inserting elements from
the input array into the set takes O(nlog2n), and processing q queries takes O(qlog2n).
Algorithm implementation – O(n + qlog2n)
Declare an array.
#define MAX
1000000
int m[MAX];
Read the input data.
scanf("%d %d",
&n, &q);
for (i = 0; i < n; i++)
scanf("%d",
&m[i]);
Process q queries sequentially.
for (i = 0; i < q; i++)
{
Read the value of x.
scanf("%d",
&x);
A number x is present in the array m
if binary_search
returns true.
if
(binary_search(m, m + n, x) == 1)
puts("YES");
else
puts("NO");
}
Algorithm implementation – lower_bound, upper_bound
Declare an array.
#define MAX
1000000
int m[MAX];
Read the input data.
scanf("%d %d",
&n, &q);
for (i = 0; i < n; i++)
scanf("%d",
&m[i]);
Process q queries sequentially.
for (i = 0; i < q; i++)
{
Read the value of x.
scanf("%d",
&x);
A number x is present in the array m
if
lower_bound(m, m + n, x)
≠ upper_bound(m, m + n,
x)
if
(lower_bound(m, m + n, x) != upper_bound(m, m + n, x))
puts("YES");
else
puts("NO");
}
Algorithm implementation – own binary search
Declare an array.
#define MAX 1000000
int m[MAX];
The my_bin_search function implements a
binary search and returns 1, if the number x is present in the array m
within the range [start; end].
int my_bin_search(int *m, int
start, int end, int x)
{
Perform a binary search on the interval [start;
end].
while
(start < end)
{
int mid
= (start + end) / 2;
if (x
> m[mid])
start
= mid + 1;
else
end =
mid;
}
Return the result.
return
m[start] == x;
}
The main part of the program. Read the input data.
scanf("%d %d",
&n, &q);
for (i = 0; i < n; i++)
scanf("%d",
&m[i]);
Process q queries sequentially.
for (i = 0; i < q; i++)
{
Read the value of x.
scanf("%d",
&x);
A number x is present in the
array m
if my_bin_search returns 1.
if
(my_bin_search(m, 0, n - 1, x))
puts("YES");
else
puts("NO");
}
Algorithm implementation – set, O(nlog2n + qlog2n)
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
int i, n, q, x;
set<int> s;
int main(void)
{
scanf("%d
%d", &n, &q);
for (i =
0; i < n; i++)
{
scanf("%d",
&x);
s.insert(x);
}
for (i =
0; i < q; i++)
{
scanf("%d",
&x);
if
(s.find(x) != s.end())
puts("YES");
else
puts("NO");
}
return 0;
}
Java implementation – own binary
search
import java.util.*;
import java.io.*;
public class Main
{
static int my_bin_search(int m[], int start, int end, int x)
{
while (start < end)
{
int mid = (start + end) /
2;
if (x > m[mid])
start = mid + 1;
else
end
= mid;
}
return (m[start] == x) ? 1 :
0;
}
public static void main(String[] args)
{
FastScanner con =
new FastScanner(new
InputStreamReader(System.in));
int n = con.nextInt();
int q = con.nextInt();
int m[] = new int[n];
for(int i = 0; i < n; i++)
m[i]
= con.nextInt();
for(int i = 0; i < q; i++)
{
int x = con.nextInt();
if(my_bin_search(m,0,n-1,x)
== 1)
System.out.println("YES");
else
System.out.println("NO");
}
}
}
class FastScanner
{
private BufferedReader br;
private StringTokenizer st;
public
FastScanner(InputStreamReader reader)
{
br = new
BufferedReader(reader);
}
public String next()
{
while (st == null ||
!st.hasMoreTokens())
{
try
{
st
= new StringTokenizer(br.readLine());
} catch (Exception e)
{
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt()
{
return
Integer.parseInt(next());
}
public double nextDouble()
{
return
Double.parseDouble(next());
}
public void close() throws Exception
{
br.close();
}
}
Java implementation – Arrays.binarySearch
import java.util.*;
import java.io.*;
public class Main
{
public static void main(String[] args)
{
FastScanner con =
new FastScanner(new
InputStreamReader(System.in));
int n = con.nextInt();
int q = con.nextInt();
int m[] = new int[n];
for(int i = 0; i < n; i++)
m[i] = con.nextInt();
for(int i = 0; i < q; i++)
{
int x = con.nextInt();
if(Arrays.binarySearch(m, x) >= 0)
System.out.println("YES");
else
System.out.println("NO");
}
}
}
class FastScanner
{
private BufferedReader br;
private StringTokenizer st;
public
FastScanner(InputStreamReader reader)
{
br = new BufferedReader(reader);
}
public String next()
{
while (st == null || !st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch (Exception e)
{
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
public double nextDouble()
{
return Double.parseDouble(next());
}
public void close() throws Exception
{
br.close();
}
}
Python implementation
Import the bisect
module.
import bisect
Read the
input data.
n, q = map(int,input().split())
lst = list(map(int,input().split()))
Process q queries sequentially.
for _ in range(q):
Read the value of x.
x = int(input())
A number x is present in the list lst if
bisect.bisect_left(lst, x) ≠ bisect.bisect_right(lst, x)
if bisect.bisect_left(lst,
x) != bisect.bisect_right(lst, x):
print("YES")
else:
print("NO")
Python implementation – own binary
search
The my_bin_search function implements a binary search:
·
If the number x is not present in
the list a, the function returns -1.
·
Otherwise, it returns the position of the
number x in the list a.
def my_bin_search(a, x):
start = 0
end = len(a) – 1
Perform a binary search over the interval [start;
end] = [0; len(a) – 1].
while start <
end:
mid = (start + end) // 2;
if x > a[mid]:
start = mid + 1;
else:
end = mid;
Return the result.
if a[start] == x:
return start
else:
return -1;
The main part of the program. Read the input data.
n, q = map(int,input().split())
lst = list(map(int,input().split()))
Process q queries sequentially.
for _ in range(q):
Read the value of x.
x = int(input())
Perform a
binary search. Print the corresponding result.
if my_bin_search(lst,x) != -1:
print("YES")
else:
print("NO")